이번에는 나무를 그려본다. 자연에서 나무가 가지를 뻗는것도 일정한 패턴을 가지고 있다고 한다. back이라는 명령이 있을까 하여 대충 써봤는데 뒤로가기도 있었네 (당연한거겠지만..-_-)
그리고 이번에는 코드에 indentation을 주어 이해가 쉽도록 했다. 한줄에 모두 적는것보다는 특정한 모양을 그리는 부분에 해당하는 부분을 같은 indentation을 주니 자연스레 코드도 점진적으로 코드를 작성하게 되었다. 일단, 나무가지가 왼쪽으로만 뻗는다고 가정했을때의 모양과 코드
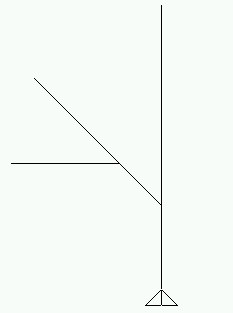
왼쪽으로만 가지치는 나무 (drawtree 300 2)
to drawtree :l :n
if :n=0 [fd :l back :l stop]
fd :l back :l
fd :l/3
lt 45 drawtree 3/5*:l :n-1 rt 45
back :l/3
end
if :n=0 [fd :l back :l stop]
fd :l back :l
fd :l/3
lt 45 drawtree 3/5*:l :n-1 rt 45
back :l/3
end
fd :l/3 ... back :/3 사이에 가지를 치는 코드를 추가하면 왼쪽으로 약간 긴 가지 한번을 치고 오를쪽으로 약간 짧은 가지를 한번 치는 나무가 된다.
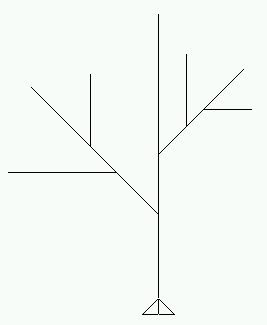
왼쪽으로 약간길게, 오른쪽으로 조금 짧게 가지치는 나무 (drawtree 300 2)
to drawtree :l :n
if :n=0 [fd :l back :l stop]
fd :l back :l
fd :l/3
lt 45 drawtree 3/5*:l :n-1 rt 45
fd :l/5
rt 45 drawtree 2/5*:l :n-1 lt 45
back :l/5
back :l/3
end
if :n=0 [fd :l back :l stop]
fd :l back :l
fd :l/3
lt 45 drawtree 3/5*:l :n-1 rt 45
fd :l/5
rt 45 drawtree 2/5*:l :n-1 lt 45
back :l/5
back :l/3
end
방금 추가된 코드와 같은 레벨에서 코드를 또 추가하면 같은 방향으로 가지를 두번 치는 나무가 된다. 그런데,, 그림이 그다지 이쁘지는 않네..-_-a
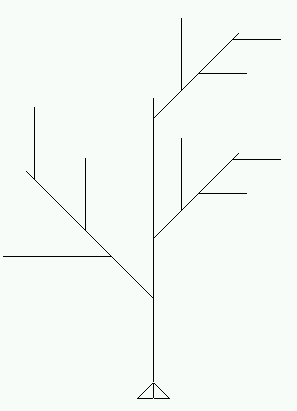
왼쪽으로 한번, 오른쪽으로 두번 가지치는 나무 (drawtree 300 2)
to drawtree :l :n
if :n=0 [fd :l back :l stop]
fd :l back :l
fd :l/3
lt 45 drawtree 3/5*:l :n-1 rt 45
fd :l/5
rt 45 drawtree 2/5*:l :n-1 lt 45
back :l/5
fd :l*3/5
rt 45 drawtree 2/5*:l :n-1 lt 45
back :l*3/5
back :l/3
end
if :n=0 [fd :l back :l stop]
fd :l back :l
fd :l/3
lt 45 drawtree 3/5*:l :n-1 rt 45
fd :l/5
rt 45 drawtree 2/5*:l :n-1 lt 45
back :l/5
fd :l*3/5
rt 45 drawtree 2/5*:l :n-1 lt 45
back :l*3/5
back :l/3
end
역시 난 미적 감각이 너무 떨어진다...-_-;;